How Ratios and Frequencies Create Harmony? – Comprehensive Guide
Harmony is often based on math, primarily on how ratios work. Music is made of notes, each with a different sound.
Harmony isn’t not related to music, it is also found in math, building, art, and the natural world. The basic idea of harmony is about how things fit together well. It’s about the relationship between different parts, the parts are like numbers that compare things and how often something happens. Together, they make things look and feel good in many different ways.
Mathematical Foundations of Harmony
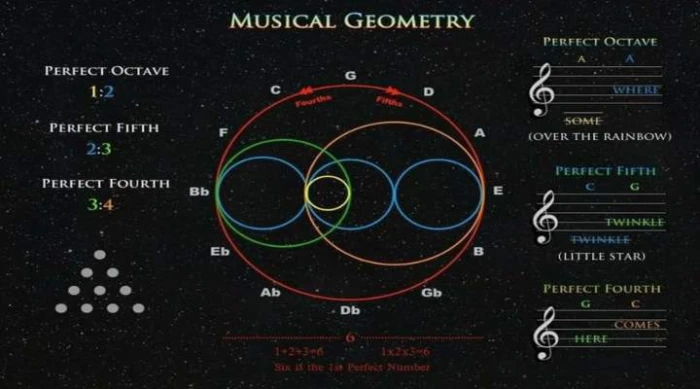
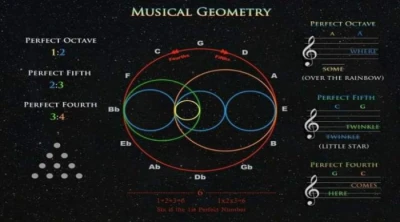
Harmony is often based on math, primarily on how ratios work. Music is made of notes, each with a different sound. When these sounds work together nicely, they create harmony. The most common ratio in music is an octave. It’s a 2:1 ratio which means one note is twice as high as another. For example, if one note sounds at 440 Hz, the note an octave higher will sound at 880 Hz. The relationship sounds good to our ears because it feels right and steady.
You might have been familiar with “perfect fifth”, if not then let’s define it here as it is an interval of seven semitones between 2 notes. Concerned music, it is a fundamental ratio in music with a frequency ratio of 3:2. When two notes are played together that maintain this ratio, they blend seamlessly, creating a harmonious sound. They synchronize together because the notes fit together mathematically. This relationship can be objectively quantified which led to the development of musical scales and systems.
The perfect fifth has been central to Western Music theory and practice for centuries. It is considered one of the most consonant intervals, means it sounds pleasing to the ears. The perfect fifth is used in various musical contexts, from simple folk songs to complex symphonies.
Perfect fifth is also a vital component of the major and minor scales which are the foundation of Western Music. The major scale is based on the perfect fifth, while the minor scale is based on a slightly different interval called the minor third. The ideal fifth creates the dominant chord, one of Western Music’s most essential chords.
Frequencies and Sound Waves
Frequencies are essential when we talk about sound. Sound is like a wave that moves through something, and how it sounds depends a lot on frequency. High frequencies make sounds higher, while low frequencies make sounds lower. When different sounds with different frequencies mix, they can make more complicated sounds. When different sounds mix, they can create harmony or dissonance.
Harmony is a pleasant sound while dissonance is unpleasant. The way these sounds mix depends on their frequencies. Musicians carefully adjust these frequencies to create the desired emotional impact on their listeners. By understanding the relationships between different frequencies, musicians can manipulate them to evoke a wide range of feelings in their audience.
Harmony in Nature – The Fibonacci sequence and the Golden Ratio
The relationship between ratios and harmony isn’t just about music, it can also be seen in nature and art. A good example is the Fibonacci sequence. In this order, every number is the total of two numbers that come before this sequence (1, 1, 2, 3, 5, 8, and so on). If we divide any number in the sequence by the number before it, we get a ratio close to the Golden Ratio about 1.618.
The Golden Ratio is a special proportion that we often see in natural patterns. For example, you can find it in the way leaves are arranged on a stem or in the spirals of shells. Many people think the Golden Ratio is a beautiful number. Artists and builders have used it to make things look nice. Famous buildings like the Parthenon and paintings by Leonardo da Vinci show this unique number. People believe that using math to make things can make them look beautiful and balanced.
Applications in Art and Architecture
In art, ratios and frequencies are fundamental. Artists often use the ideas of proportion and symmetry to make their work look good. For example, the Rule of Thirds in photography divides a picture into nine equal parts, helping to make the image look good by putting things of interest along the lines or where they cross.
Similarly, harmonious designs in architecture often incorporate ratios and frequencies to evoke a sense of stability and beauty. The Parthenon’s dimensions and the proportions of its columns exemplify this application. The careful consideration of ratios ensures that buildings aren’t only functional but also aesthetically pleasing.
Psychological and Emotional Impact
Impact of ratios and frequencies on harmony extends to psychological and emotional dimensions. Studies have shown that music can evoke a range of emotions based on the harmony created by specific ratios and frequencies. Harmonious music is often associated with feelings of joy and peace while dissonant music can evoke tension and unease. This emotional response underscores the profound connection between mathematical relationships and human experiences. Further, we’ll explore how ratios and frequencies contribute to create harmony across various domains.
Color Harmony and Light Frequency
Color harmony is often understood through the science of light and its frequencies. Light consists of electromagnetic waves and each color in the visible spectrum corresponds to a different frequency of light. When specific colors are combined, their frequencies form harmonious patterns that are visually pleasing.
The relationship between color and light frequency also ties into the resonance phenomenon, where specific wavelengths enhance one another. Artists and designers often rely on color harmony to create balanced visual compositions. In design, the understanding of color harmony, rooted in the ratios of light frequencies, enables creators to evoke certain moods and emotions, using combinations that either soothe or energize viewers.
Ratio of Harmonies in Music
In music, harmony is created through the ratio of frequencies between different notes. The most harmonious combination of notes, known as consonances, are based on simple frequency ratios. This ratio is universally perceived as stable and pleasing. Similarly, the perfect fifth, another consonant interval, has a ratio of 3:2.
In contrast, the ideal fourth has a ratio of 4:3. These superficial mathematical relationships between frequencies produce harmonious sounds because the waveforms of the notes align in predictable, repeating patterns, reducing dissonance. Musicians often use these principles to create chords and melodies that are aesthetically pleasing, relying on the ratios of frequencies to guide their composition.
Harmony with Proportions in Art and Design
In art and design, harmony is achieved not just through color but also through proportions. The ancient Greeks discovered that specific proportions such as the Golden Ratio (1.618:1), are inherently pleasing to the human eye. This ratio appears in nature, architecture, and art, creating balance and harmony.
The golden ratio can be seen in the proportions of the Parthenon in Athens, the spiral of a seashell, and the arrangement of petals in a flower. Design proportions are often based on mathematical relationships that mirror those found in nature. These harmonious proportions create visual equilibrium where no element dominates the composition, allowing the viewer to experience a sense of calm and beauty. Artists and architects who understand how to apply these ratios can create works that resonate with the natural human preference for harmony.
Ratio of Frequencies in Physics
In physics, frequencies are integral to understanding how harmony occurs in various phenomena. Whether its sound waves, light waves, or even the movement of planets, everything vibrates at different frequencies. The ratios between these frequencies can create harmonious interactions.
For instance, when two sounds have frequencies that relate to each other by simple ratios, they produce a harmonious sound in acoustics. This is because the sound waves align in a way that reduces interference, creating a smooth and continuous waveform. In astronomy, Johannes Kepler’s Music of the Spheres described how planets’ orbits follow harmonic ratios; much like notes on a musical scale. These ratios between celestial bodies’ orbital periods create a form of cosmic harmony, reinforcing the idea that the interplay of frequencies and ratios governs the universe itself.
Sine Waves Create Harmony in Sound and Light
A sine wave is the most fundamental waveform in both sound and light. It represents a pure frequency without any harmonics or overtones. In music, a sine wave produces a smooth, continuous tone, and when multiple sine waves with frequencies related by simple ratios are combined, they create harmonious sounds.
Whether in sync or out of phase, the relationship between these waves determines whether the sound will be harmonious or dissonant. In light, sine waves also play a crucial role in creating harmony. Different light frequencies can be combined to create white light which the human eye perceives as harmonious. The balance of these frequencies, represented by sine waves, allows for a coherent unified perception of light.
Harmony of Mathematical Shapes
Harmony is also found in the realm of mathematics through geometric shapes and their ratios. Regular polygons, circles, and spirals all exhibit mathematical harmony in their proportions. For example, a circle’s circumference and diameter are related by the ratio π (value is approximately 3.14), a constant that governs much of geometry. In nature, the Fibonacci sequence which is closely related to the golden ratio, manifests in the arrangement of trees, branching of leaves, and the structure of galaxies. The recurrence of these harmonious shapes in nature reflects the deep mathematical relationships that underpin the physical world.
In short, ratios and frequencies help make things sound, look, or feel good. They are like the building blocks of harmony in music, art, and nature. These numbers show us how to make things balanced and beautiful. By understanding how they work, we can appreciate art and nature more and enjoy our lives better. If we pay attention to these numbers, we can see the beauty and balance all around us.
Use the Bandwidth Calculator to assess the required bandwidth for your business needs. Start by going to the bandwidth calculator page and optimize your network performance.
Harmony isn’t not related to music, it is also found in math, building, art, and the natural world. The basic idea of harmony is about how things fit together well. It’s about the relationship between different parts, the parts are like numbers that compare things and how often something happens. Together, they make things look and feel good in many different ways.
Mathematical Foundations of Harmony
Harmony is often based on math, primarily on how ratios work. Music is made of notes, each with a different sound. When these sounds work together nicely, they create harmony. The most common ratio in music is an octave. It’s a 2:1 ratio which means one note is twice as high as another. For example, if one note sounds at 440 Hz, the note an octave higher will sound at 880 Hz. The relationship sounds good to our ears because it feels right and steady.
You might have been familiar with “perfect fifth”, if not then let’s define it here as it is an interval of seven semitones between 2 notes. Concerned music, it is a fundamental ratio in music with a frequency ratio of 3:2. When two notes are played together that maintain this ratio, they blend seamlessly, creating a harmonious sound. They synchronize together because the notes fit together mathematically. This relationship can be objectively quantified which led to the development of musical scales and systems.
The perfect fifth has been central to Western Music theory and practice for centuries. It is considered one of the most consonant intervals, means it sounds pleasing to the ears. The perfect fifth is used in various musical contexts, from simple folk songs to complex symphonies.
Perfect fifth is also a vital component of the major and minor scales which are the foundation of Western Music. The major scale is based on the perfect fifth, while the minor scale is based on a slightly different interval called the minor third. The ideal fifth creates the dominant chord, one of Western Music’s most essential chords.
Frequencies and Sound Waves
Frequencies are essential when we talk about sound. Sound is like a wave that moves through something, and how it sounds depends a lot on frequency. High frequencies make sounds higher, while low frequencies make sounds lower. When different sounds with different frequencies mix, they can make more complicated sounds. When different sounds mix, they can create harmony or dissonance.
Harmony is a pleasant sound while dissonance is unpleasant. The way these sounds mix depends on their frequencies. Musicians carefully adjust these frequencies to create the desired emotional impact on their listeners. By understanding the relationships between different frequencies, musicians can manipulate them to evoke a wide range of feelings in their audience.
Harmony in Nature – The Fibonacci sequence and the Golden Ratio
The relationship between ratios and harmony isn’t just about music, it can also be seen in nature and art. A good example is the Fibonacci sequence. In this order, every number is the total of two numbers that come before this sequence (1, 1, 2, 3, 5, 8, and so on). If we divide any number in the sequence by the number before it, we get a ratio close to the Golden Ratio about 1.618.
The Golden Ratio is a special proportion that we often see in natural patterns. For example, you can find it in the way leaves are arranged on a stem or in the spirals of shells. Many people think the Golden Ratio is a beautiful number. Artists and builders have used it to make things look nice. Famous buildings like the Parthenon and paintings by Leonardo da Vinci show this unique number. People believe that using math to make things can make them look beautiful and balanced.
Applications in Art and Architecture
In art, ratios and frequencies are fundamental. Artists often use the ideas of proportion and symmetry to make their work look good. For example, the Rule of Thirds in photography divides a picture into nine equal parts, helping to make the image look good by putting things of interest along the lines or where they cross.
Similarly, harmonious designs in architecture often incorporate ratios and frequencies to evoke a sense of stability and beauty. The Parthenon’s dimensions and the proportions of its columns exemplify this application. The careful consideration of ratios ensures that buildings aren’t only functional but also aesthetically pleasing.
Psychological and Emotional Impact
Impact of ratios and frequencies on harmony extends to psychological and emotional dimensions. Studies have shown that music can evoke a range of emotions based on the harmony created by specific ratios and frequencies. Harmonious music is often associated with feelings of joy and peace while dissonant music can evoke tension and unease. This emotional response underscores the profound connection between mathematical relationships and human experiences. Further, we’ll explore how ratios and frequencies contribute to create harmony across various domains.
Color Harmony and Light Frequency
Color harmony is often understood through the science of light and its frequencies. Light consists of electromagnetic waves and each color in the visible spectrum corresponds to a different frequency of light. When specific colors are combined, their frequencies form harmonious patterns that are visually pleasing.
The relationship between color and light frequency also ties into the resonance phenomenon, where specific wavelengths enhance one another. Artists and designers often rely on color harmony to create balanced visual compositions. In design, the understanding of color harmony, rooted in the ratios of light frequencies, enables creators to evoke certain moods and emotions, using combinations that either soothe or energize viewers.
Ratio of Harmonies in Music
In music, harmony is created through the ratio of frequencies between different notes. The most harmonious combination of notes, known as consonances, are based on simple frequency ratios. This ratio is universally perceived as stable and pleasing. Similarly, the perfect fifth, another consonant interval, has a ratio of 3:2.
In contrast, the ideal fourth has a ratio of 4:3. These superficial mathematical relationships between frequencies produce harmonious sounds because the waveforms of the notes align in predictable, repeating patterns, reducing dissonance. Musicians often use these principles to create chords and melodies that are aesthetically pleasing, relying on the ratios of frequencies to guide their composition.
Harmony with Proportions in Art and Design
In art and design, harmony is achieved not just through color but also through proportions. The ancient Greeks discovered that specific proportions such as the Golden Ratio (1.618:1), are inherently pleasing to the human eye. This ratio appears in nature, architecture, and art, creating balance and harmony.
The golden ratio can be seen in the proportions of the Parthenon in Athens, the spiral of a seashell, and the arrangement of petals in a flower. Design proportions are often based on mathematical relationships that mirror those found in nature. These harmonious proportions create visual equilibrium where no element dominates the composition, allowing the viewer to experience a sense of calm and beauty. Artists and architects who understand how to apply these ratios can create works that resonate with the natural human preference for harmony.
Ratio of Frequencies in Physics
In physics, frequencies are integral to understanding how harmony occurs in various phenomena. Whether its sound waves, light waves, or even the movement of planets, everything vibrates at different frequencies. The ratios between these frequencies can create harmonious interactions.
For instance, when two sounds have frequencies that relate to each other by simple ratios, they produce a harmonious sound in acoustics. This is because the sound waves align in a way that reduces interference, creating a smooth and continuous waveform. In astronomy, Johannes Kepler’s Music of the Spheres described how planets’ orbits follow harmonic ratios; much like notes on a musical scale. These ratios between celestial bodies’ orbital periods create a form of cosmic harmony, reinforcing the idea that the interplay of frequencies and ratios governs the universe itself.
Sine Waves Create Harmony in Sound and Light
A sine wave is the most fundamental waveform in both sound and light. It represents a pure frequency without any harmonics or overtones. In music, a sine wave produces a smooth, continuous tone, and when multiple sine waves with frequencies related by simple ratios are combined, they create harmonious sounds.
Whether in sync or out of phase, the relationship between these waves determines whether the sound will be harmonious or dissonant. In light, sine waves also play a crucial role in creating harmony. Different light frequencies can be combined to create white light which the human eye perceives as harmonious. The balance of these frequencies, represented by sine waves, allows for a coherent unified perception of light.
Harmony of Mathematical Shapes
Harmony is also found in the realm of mathematics through geometric shapes and their ratios. Regular polygons, circles, and spirals all exhibit mathematical harmony in their proportions. For example, a circle’s circumference and diameter are related by the ratio π (value is approximately 3.14), a constant that governs much of geometry. In nature, the Fibonacci sequence which is closely related to the golden ratio, manifests in the arrangement of trees, branching of leaves, and the structure of galaxies. The recurrence of these harmonious shapes in nature reflects the deep mathematical relationships that underpin the physical world.
In short, ratios and frequencies help make things sound, look, or feel good. They are like the building blocks of harmony in music, art, and nature. These numbers show us how to make things balanced and beautiful. By understanding how they work, we can appreciate art and nature more and enjoy our lives better. If we pay attention to these numbers, we can see the beauty and balance all around us.
Use the Bandwidth Calculator to assess the required bandwidth for your business needs. Start by going to the bandwidth calculator page and optimize your network performance.
Conversation
Latest Blogs
© Blog CoolCalculator, Explore CoolCalculator, your destination for the latest insights, tips, and updates on the world of online calculators. Stay informed and make your calculations smarter with our blog. ,
Designed
by Saad Media Team , Team Lead M.Rizwan Akhtar