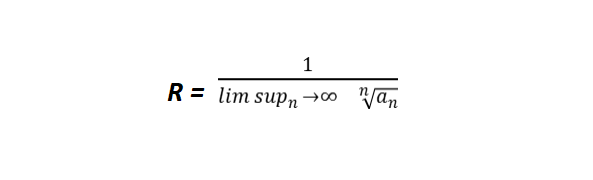Important Aspects Related to Interval of Convergence Calculator
In math, the interval of convergence is significant when working with power series.

In math, the interval of convergence is significant when working with power series. A power series is a sum that goes on forever and looks like as mentioned below.
∑∞n=0 an (x-c)n
Where an, the area coefficient is the center of the series, and x is a variable. The interval of convergence refers to the set of all x-values for which this series converges. Determining this interval is crucial for understanding the behavior of the series and ensuring its practical utility in various applications, such as solving differential equations, modeling phenomena in physics, and analyzing functions in engineering.
An interval of convergence calculator is essential for mathematicians, scientists, and engineers as it simplifies finding the interval where a power series converges. This tool typically employs several mathematical techniques and algorithms to determine the precise range of x-values, thus, saving time and reducing the potential for error. To fully appreciate the importance of such a calculator, it's necessary to delve into the fundamental concepts related to the interval of convergence, how to find it, the role of the radius of convergence, and the implications these have in practical and theoretical contexts.
Interval of Convergence Calculator
An interval of convergence calculator is a specialized computational tool designed to help determine the range of x-values for which a given power series converges. This tool automates the complex and often tedious process of calculating convergence intervals, making it accessible for users who might not have an extensive background in advanced mathematics.
Key Features of an Interval of Convergence Calculator
- Automation of Calculations
By inputting the series and its coefficients, the calculator can quickly process the information and return the interval of convergence.
- Accuracy and Precision
These calculators use proven math methods to ensure correct results.
- User Friendly Interface
Most calculators have a straightforward interface, allowing users to easily input data and interpret results without understanding the underlying algorithms.
Manually Finding the Interval of Convergence
Finding the interval of convergence involves determining the set of all x-values for which a power series converges. This process typically includes several steps.
- Radio Test or Root Test
These are the most common methods used to determine the series' convergence. The ratio test checks the limit of the absolute value of the ratio between one term and the next in a sequence.
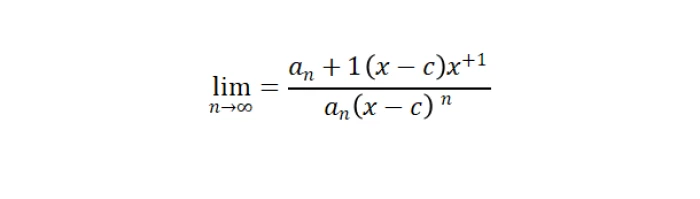
If this limit is less than 1, the series converges.
- Determining the Radius of Convergence R
This is derived from the limit found using the ratio or root test. The radius of convergence is the distance from the center to the boundary points of the interval where the series converges.
- Testing Endpoints
Once the radius of convergence is found, the endpoints of the interval [c - R, c + R] must be tested individually to determine whether they should be included in the interval of convergence. This involves substituting the endpoints into the series and checking for convergence using various convergence tests (such as the alternating series test, p-series test, etc.)
- Combining Results
The interval of convergence is then constructed by combining the results from the previous steps. If both endpoints converge, they are included in the interval; if not, they are excluded.
Find Interval of Convergence of Power Series
Finding the interval of convergence specifically for power series involves the same general steps as outlined above but is tailored to its specific characteristics. The steps involved are given below.
- Identify the Power Series
Start with the given power series.
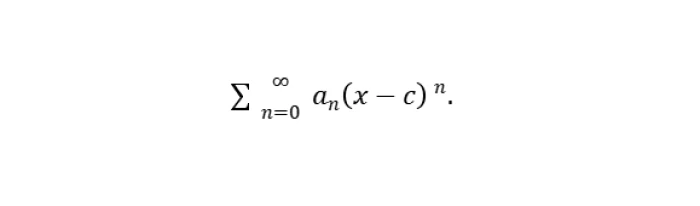
- Apply the Ratio Test
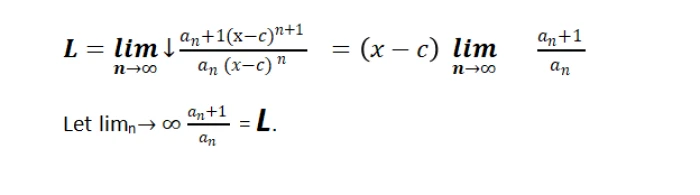
This series converges if (x - c) L < 1, which implies the following.
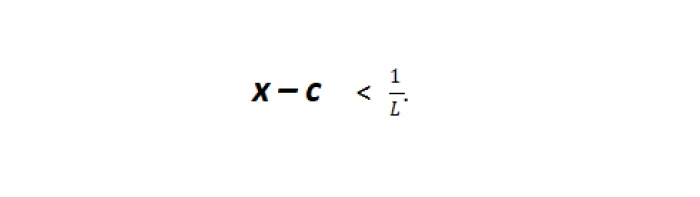
- Calculate the Radius of Convergence R
R = 1 / L
The interval of convergence is (c - R, c + R).
- Test the Endpoints
Substitue c ± R into the original series to check for convergence at these points. This may involve additional tests depending on the series' nature at these points.
- Compile the Interval
Based on the results from the endpoint tests, determine whether the endpoints are included or excluded, thus, forming the interval of convergence.
Application of the Interval of Convergence Calculator
- Educational Tool
Helps students and educators teach and learn about power series and their properties.
- Research
Assists researchers in fields like mathematics, physics, and engineering where power series are frequently used.
- Practical Problem Solving
Useful in applied mathematics for solving differential equations and modeling real-world phenomena.
Find the Radius of Convergence
The radius of convergence R is a crucial concept related to the interval of convergence. It represents the distance from the center C of the power series to the points where it ceases to converge.
Calculation Methods
- Ratio Test
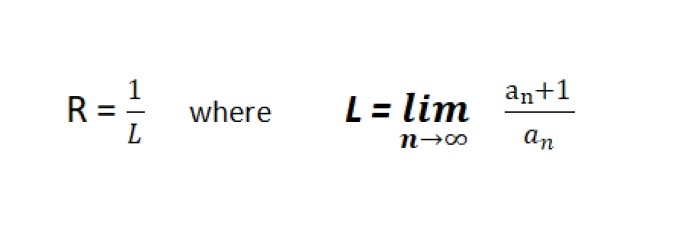
This is the most commonly used method and provides a straightforward way to find the radius of convergence.
- Root Test
This method is useful when the ratio test is inconclusive or when the series co-efficients an Image have a form that makes the root test easier to apply.
Significance of Interval of Convergence
- Determines the Interval of Convergence
Once the radius of convergence is known, it directly influences the interval by setting the bounds within which the series converges.
- Helps in Understanding Series Behavior
Knowing R provides insight into how rapidly the terms of the series decrease and thus, how quickly the series converges.
Understanding the interval of convergence is essential for working with power series in math and its applications. An interval of convergence calculator is a helpful tool that is precise, efficient, and easy to use.
The interval of convergence calculator is a valuable tool. It makes studying and using power series easier and more efficient. Understanding and using the interval of convergence is very important for getting the best results from power series in different areas like education, research, and real-life applications.
Also, have a look at the passive income ideas that can help you achieve your financial goals.

In math, the interval of convergence is significant when working with power series. A power series is a sum that goes on forever and looks like as mentioned below.
∑∞n=0 an (x-c)n
Where an, the area coefficient is the center of the series, and x is a variable. The interval of convergence refers to the set of all x-values for which this series converges. Determining this interval is crucial for understanding the behavior of the series and ensuring its practical utility in various applications, such as solving differential equations, modeling phenomena in physics, and analyzing functions in engineering.
An interval of convergence calculator is essential for mathematicians, scientists, and engineers as it simplifies finding the interval where a power series converges. This tool typically employs several mathematical techniques and algorithms to determine the precise range of x-values, thus, saving time and reducing the potential for error. To fully appreciate the importance of such a calculator, it's necessary to delve into the fundamental concepts related to the interval of convergence, how to find it, the role of the radius of convergence, and the implications these have in practical and theoretical contexts.
Interval of Convergence Calculator
An interval of convergence calculator is a specialized computational tool designed to help determine the range of x-values for which a given power series converges. This tool automates the complex and often tedious process of calculating convergence intervals, making it accessible for users who might not have an extensive background in advanced mathematics.
Key Features of an Interval of Convergence Calculator
- Automation of Calculations
By inputting the series and its coefficients, the calculator can quickly process the information and return the interval of convergence.
- Accuracy and Precision
These calculators use proven math methods to ensure correct results.
- User Friendly Interface
Most calculators have a straightforward interface, allowing users to easily input data and interpret results without understanding the underlying algorithms.
Manually Finding the Interval of Convergence
Finding the interval of convergence involves determining the set of all x-values for which a power series converges. This process typically includes several steps.
- Radio Test or Root Test
These are the most common methods used to determine the series' convergence. The ratio test checks the limit of the absolute value of the ratio between one term and the next in a sequence.
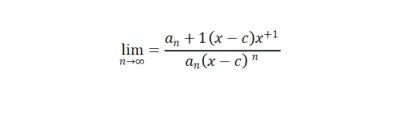
If this limit is less than 1, the series converges.
- Determining the Radius of Convergence R
This is derived from the limit found using the ratio or root test. The radius of convergence is the distance from the center to the boundary points of the interval where the series converges.
- Testing Endpoints
Once the radius of convergence is found, the endpoints of the interval [c - R, c + R] must be tested individually to determine whether they should be included in the interval of convergence. This involves substituting the endpoints into the series and checking for convergence using various convergence tests (such as the alternating series test, p-series test, etc.)
- Combining Results
The interval of convergence is then constructed by combining the results from the previous steps. If both endpoints converge, they are included in the interval; if not, they are excluded.
Find Interval of Convergence of Power Series
Finding the interval of convergence specifically for power series involves the same general steps as outlined above but is tailored to its specific characteristics. The steps involved are given below.
- Identify the Power Series
Start with the given power series.
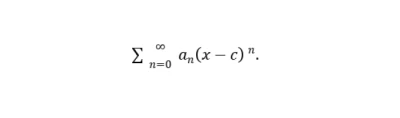
- Apply the Ratio Test
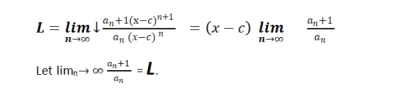
This series converges if (x - c) L < 1, which implies the following.
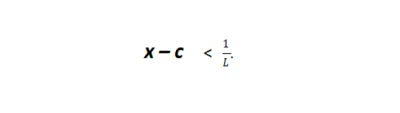
- Calculate the Radius of Convergence R
R = 1 / L
The interval of convergence is (c - R, c + R).
- Test the Endpoints
Substitue c ± R into the original series to check for convergence at these points. This may involve additional tests depending on the series' nature at these points.
- Compile the Interval
Based on the results from the endpoint tests, determine whether the endpoints are included or excluded, thus, forming the interval of convergence.
Application of the Interval of Convergence Calculator
- Educational Tool
Helps students and educators teach and learn about power series and their properties.
- Research
Assists researchers in fields like mathematics, physics, and engineering where power series are frequently used.
- Practical Problem Solving
Useful in applied mathematics for solving differential equations and modeling real-world phenomena.
Find the Radius of Convergence
The radius of convergence R is a crucial concept related to the interval of convergence. It represents the distance from the center C of the power series to the points where it ceases to converge.
Calculation Methods
- Ratio Test
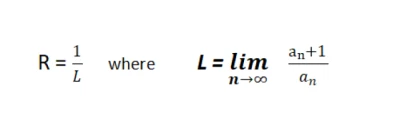
This is the most commonly used method and provides a straightforward way to find the radius of convergence.
- Root Test
This method is useful when the ratio test is inconclusive or when the series co-efficients an Image have a form that makes the root test easier to apply.
Significance of Interval of Convergence
- Determines the Interval of Convergence
Once the radius of convergence is known, it directly influences the interval by setting the bounds within which the series converges.
- Helps in Understanding Series Behavior
Knowing R provides insight into how rapidly the terms of the series decrease and thus, how quickly the series converges.
Understanding the interval of convergence is essential for working with power series in math and its applications. An interval of convergence calculator is a helpful tool that is precise, efficient, and easy to use.
The interval of convergence calculator is a valuable tool. It makes studying and using power series easier and more efficient. Understanding and using the interval of convergence is very important for getting the best results from power series in different areas like education, research, and real-life applications.
Also, have a look at the passive income ideas that can help you achieve your financial goals.
Conversation
Latest Blogs
© Blog CoolCalculator, Explore CoolCalculator, your destination for the latest insights, tips, and updates on the world of online calculators. Stay informed and make your calculations smarter with our blog. ,
Designed
by Saad Media Team , Team Lead M.Rizwan Akhtar