Prime Factorization Methods and Exponential Factorization Techniques
Find out how trial division, factor trees, and the Sieve of Eratosthenes can help you determine the prime factors of a number, as well as how exponential factorization simplifies complex expressions.

Prime Factorization
Prime factorization involves determining the prime factors of a number, meaning the fundamental prime numbers that, when multiplied together, result in the original number. This process is beneficial for composite numbers, which have more than two factors. It's important to note that prime factorization isn't applicable to prime numbers, as they only have two factors - 1 and the number itself. We offer a user-friendly online prime factorization calculator to assist you in your daily math.
Trial Division
In trial division, you begin with the smallest prime number, like 2, and divide the given number by it. Keep dividing by prime numbers until the quotient can no longer be evenly divided. Move on to the next prime number and repeat the process until the quotient becomes 1. The divisors you use in this process end up being the prime factorization of the original number. It's like breaking down the number step by step, using primes as building blocks until you've accounted for all the factors.
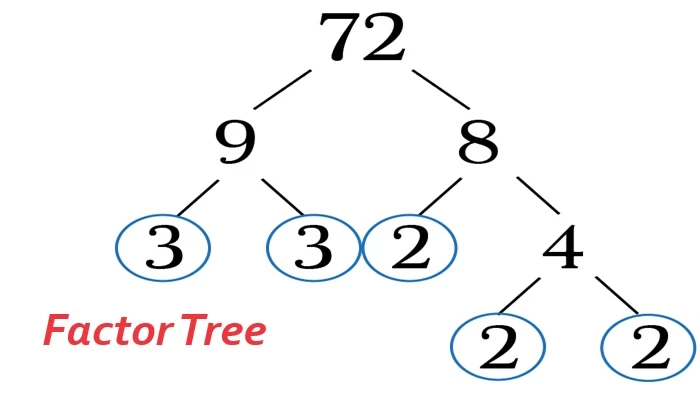
Factor Tree
The factor tree method is a visual and systematic approach used in mathematics to factorize a given number into its prime factors. It involves breaking down a number into its prime components through a series of branches resembling the structure of a tree. To start, the given number is represented at the top of the tree, and then it is progressively divided into its prime factors. At each step, the number is factored into two or more factors, and the process continues until the factors are prime numbers. The branches of the tree represent the successive divisions, making it easy to see the prime factorization of the original number. This method is particularly useful for understanding the fundamental building blocks of a number. It provides a clear visual representation of prime factorization, aiding in various mathematical applications such as simplifying fractions or solving equations. The factor tree method is a valuable tool that not only helps in factorization but also enhances comprehension of number theory concepts.
Prime Factorization by Division

In this approach, which is similar to trial division, the method involves employing only prime divisors rather than all primes. Start by dividing the number in question by its smallest prime divisor, then repeat the process with the quotient and the subsequent prime divisors until the quotient eventually becomes another way to compute this is by using our LCM Calculator.
Sieve of Eratosthenes
The Sieve of Eratosthenes is a classic method for finding all prime numbers up to a given limit. Still, it can also be adapted for prime factorization. Let's break it down. Imagine you want to find the prime factorization of a number, say 48. First, you create a list of numbers from 2 to 48. Now, you start with the smallest prime number, which is 2, and cross out all multiples of 2 in the list, except 2 itself. In this case, you'd cross out 4, 6, 8, and so on, but leave 2 untouched. Then, you move on to the next number in the list that has yet to be crossed out, which is 3, and repeat the process. Continue this until you've gone through all the numbers in the list.
After completing the process, the remaining numbers in the list that still need to be crossed out are prime numbers. In our example, those would be 2, 3, 5, 7, 11, and so on. Now, to find the prime factorization of 48, you look at these primes and divide 48 by them in order.
Exponential Factorization
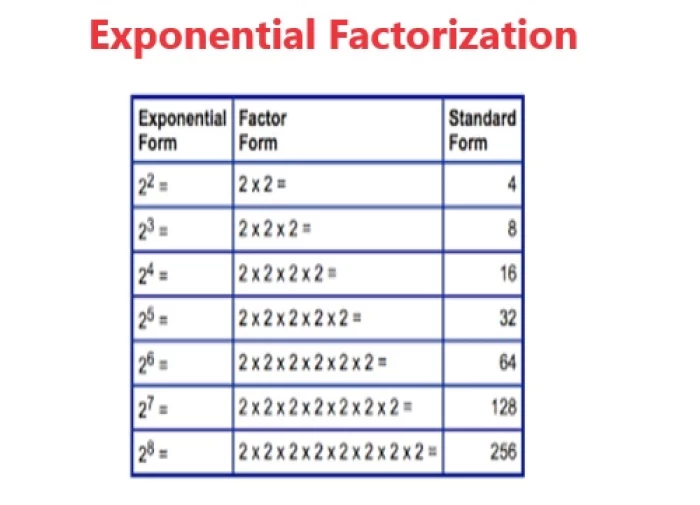
Exponential factorization is a mathematical process that involves breaking down an expression with exponential terms into simpler, more manageable components. This technique is beneficial when dealing with expressions that involve multiplication or division of exponential terms with the same base. To factorize an exponential expression, you can use the laws of exponents. For instance, consider the expression 2^3 * 2^5. By applying the law of exponents, which states that when you multiply two exponential terms with the same base, you add their exponents, you can factorize this expression as 2^(3+5), resulting in 2^8. This shows that the original expression can be simplified to a single exponential term with a combined exponent. Exponential factorization helps streamline calculations and enhances the understanding of the relationships between different exponential terms within an expression. Our exponential calculator further helps you with measures related to exponential expressions.

Prime Factorization
Prime factorization involves determining the prime factors of a number, meaning the fundamental prime numbers that, when multiplied together, result in the original number. This process is beneficial for composite numbers, which have more than two factors. It's important to note that prime factorization isn't applicable to prime numbers, as they only have two factors - 1 and the number itself. We offer a user-friendly online prime factorization calculator to assist you in your daily math.
Trial Division
In trial division, you begin with the smallest prime number, like 2, and divide the given number by it. Keep dividing by prime numbers until the quotient can no longer be evenly divided. Move on to the next prime number and repeat the process until the quotient becomes 1. The divisors you use in this process end up being the prime factorization of the original number. It's like breaking down the number step by step, using primes as building blocks until you've accounted for all the factors.
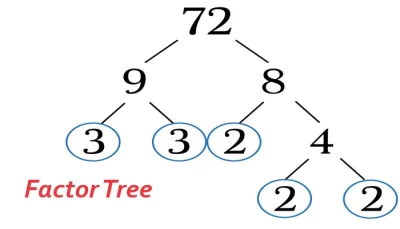
Factor Tree
The factor tree method is a visual and systematic approach used in mathematics to factorize a given number into its prime factors. It involves breaking down a number into its prime components through a series of branches resembling the structure of a tree. To start, the given number is represented at the top of the tree, and then it is progressively divided into its prime factors. At each step, the number is factored into two or more factors, and the process continues until the factors are prime numbers. The branches of the tree represent the successive divisions, making it easy to see the prime factorization of the original number. This method is particularly useful for understanding the fundamental building blocks of a number. It provides a clear visual representation of prime factorization, aiding in various mathematical applications such as simplifying fractions or solving equations. The factor tree method is a valuable tool that not only helps in factorization but also enhances comprehension of number theory concepts.
Prime Factorization by Division

In this approach, which is similar to trial division, the method involves employing only prime divisors rather than all primes. Start by dividing the number in question by its smallest prime divisor, then repeat the process with the quotient and the subsequent prime divisors until the quotient eventually becomes another way to compute this is by using our LCM Calculator.
Sieve of Eratosthenes
The Sieve of Eratosthenes is a classic method for finding all prime numbers up to a given limit. Still, it can also be adapted for prime factorization. Let's break it down. Imagine you want to find the prime factorization of a number, say 48. First, you create a list of numbers from 2 to 48. Now, you start with the smallest prime number, which is 2, and cross out all multiples of 2 in the list, except 2 itself. In this case, you'd cross out 4, 6, 8, and so on, but leave 2 untouched. Then, you move on to the next number in the list that has yet to be crossed out, which is 3, and repeat the process. Continue this until you've gone through all the numbers in the list.
After completing the process, the remaining numbers in the list that still need to be crossed out are prime numbers. In our example, those would be 2, 3, 5, 7, 11, and so on. Now, to find the prime factorization of 48, you look at these primes and divide 48 by them in order.
Exponential Factorization
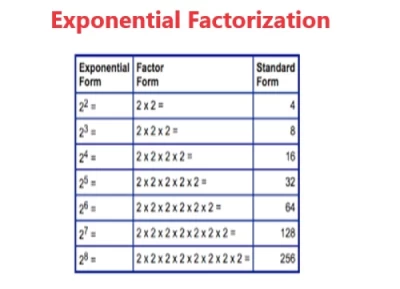
Exponential factorization is a mathematical process that involves breaking down an expression with exponential terms into simpler, more manageable components. This technique is beneficial when dealing with expressions that involve multiplication or division of exponential terms with the same base. To factorize an exponential expression, you can use the laws of exponents. For instance, consider the expression 2^3 * 2^5. By applying the law of exponents, which states that when you multiply two exponential terms with the same base, you add their exponents, you can factorize this expression as 2^(3+5), resulting in 2^8. This shows that the original expression can be simplified to a single exponential term with a combined exponent. Exponential factorization helps streamline calculations and enhances the understanding of the relationships between different exponential terms within an expression. Our exponential calculator further helps you with measures related to exponential expressions.
Conversation
Latest Blogs
© Blog CoolCalculator, Explore CoolCalculator, your destination for the latest insights, tips, and updates on the world of online calculators. Stay informed and make your calculations smarter with our blog. ,
Designed
by Saad Media Team , Team Lead M.Rizwan Akhtar