Unveiling the Secrets of Random Number Generators
In the World of Computing and Statistical Analysis
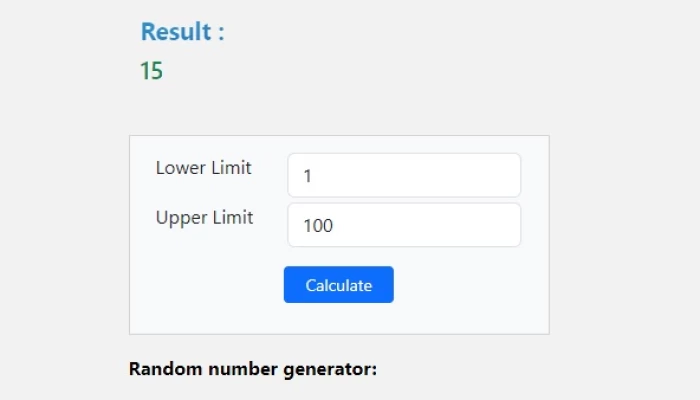
In the realm of computing and statistical analysis, the Random Number Generator (RNG) emerges as a fundamental tool, playing a pivotal role in diverse applications. This sophisticated algorithmic mechanism is designed to generate sequences of numbers devoid of any discernible pattern, exhibiting the characteristics of true randomness. The significance of RNGs extends across various domains, including cryptography, gaming, simulations, and scientific research. Understanding the inner workings of these generators is paramount, as they underpin the integrity of cryptographic protocols, ensure fairness in gaming scenarios, and contribute to the robustness of simulations. As we delve into the intricacies of random number generation, we will explore the methodologies, challenges, and the pervasive influence of RNGs in shaping the landscape of modern computing. Join us on this intellectual journey as we unravel the enigma of randomness in the digital realm.
Historical Background: A Journey Through Time
Imagine stepping back in time, long before the age of computers and smartphones. The need for randomness persisted for various activities such as games, divination, and decision-making. In the absence of algorithms and electronic gadgets, people got creative. Casting lots, rolling dice, or using wheel-like devices called "volvelles" were ancient methods of introducing an element of chance. Fast forward to the Middle Ages, where wheel-like devices evolved into "volvelles," and people continued finding new ways to generate randomness. Drawing straws or picking names from a hat became simple yet effective ways to inject unpredictability into situations. The 20th century ushered in computers, leading to the development of algorithms simulating randomness, giving birth to modern Random Number Generators (RNGs). While the methods evolved, the essence remained the same – creating randomness when needed, now hidden within the circuits of electronic devices.

Understanding the Magic of RNGs
RNGs are like magical machines creating sequences of numbers that appear random. Imagine a friend who loves playing video games; sometimes, the game needs unexpected events, like deciding where a treasure chest appears. That's where Pseudo-Random Number Generators (PRNGs) come in. They follow a plan, called a PRNG algorithm, to create a sequence of numbers that looks random. Here's the twist – they don't start from scratch each time; instead, they begin with a seed, a starting point for the magic. Changing the seed makes the numbers different, much like planting different seeds in a garden. PRNGs have come a long way from ancient lots and medieval volvelles, but the essence remains – creating randomness when needed, now in the hidden circuits of electronic devices.
Real-Life Applications of RNGs: Beyond the Digital Realm
- Cryptography: RNGs are crucial for generating cryptographic keys and initialization vectors, ensuring secure communication and data protection.
- Password Generation: RNGs can be used to generate solid and unpredictable passwords, enhancing the security of user accounts.
- Monte Carlo Simulations: RNGs are extensively used in simulations for modelling complex systems in various fields, such as finance, physics, and engineering.
- Game Development: RNGs are essential for creating unpredictable and dynamic elements in video games, such as random enemy behaviour or item drops.
- Polling and Surveys: RNGs are employed in selecting random samples for surveys and polls to ensure representativity.
- Quality Control: In manufacturing and production, RNGs are used for random sampling to test the quality of products.
- Stock Market: RNGs are used in financial models and simulations to analyze market trends, risk, and uncertainty.
- Option Pricing: In the field of finance, RNGs play a role in the Monte Carlo simulation methods used for option pricing.
- Casinos: RNGs are crucial for ensuring fairness in casino games, determining outcomes randomly and unpredictably.
- Lotteries: Random number generators are used to select winning numbers in lotteries, ensuring a fair and unbiased selection process.
- Experimentation: RNGs are employed in scientific experiments that require randomization, such as assigning subjects to different groups in a clinical trial.
- Data Analysis: RNGs are used in statistical analysis and hypothesis testing to ensure that data is randomly selected for analysis.
- Training Data Shuffling: In machine learning, RNGs are used to shuffle datasets to prevent the model from learning spurious patterns based on the order of data.
- Random Initialization: RNGs are used to initialize the weights of neural networks, helping to avoid convergence to suboptimal solutions during training.
- Search Algorithms: RNGs can be used in randomized algorithms for optimization and searching problems.
- Graph Algorithms: Randomized algorithms are employed in graph theory for tasks such as random graph generation and analysis.
- Software Testing: RNGs are used in software testing to introduce randomness and variability, helping identify potential issues and vulnerabilities.
- Procedural Generation: RNGs are used in creative fields, such as procedural generation in computer graphics and game design, to create diverse and exciting content.
For a diverse range of calculators, make sure to explore CoolCalculator and discover handy tools for various calculations.
In the realm of computing and statistical analysis, the Random Number Generator (RNG) emerges as a fundamental tool, playing a pivotal role in diverse applications. This sophisticated algorithmic mechanism is designed to generate sequences of numbers devoid of any discernible pattern, exhibiting the characteristics of true randomness. The significance of RNGs extends across various domains, including cryptography, gaming, simulations, and scientific research. Understanding the inner workings of these generators is paramount, as they underpin the integrity of cryptographic protocols, ensure fairness in gaming scenarios, and contribute to the robustness of simulations. As we delve into the intricacies of random number generation, we will explore the methodologies, challenges, and the pervasive influence of RNGs in shaping the landscape of modern computing. Join us on this intellectual journey as we unravel the enigma of randomness in the digital realm.
Historical Background: A Journey Through Time
Imagine stepping back in time, long before the age of computers and smartphones. The need for randomness persisted for various activities such as games, divination, and decision-making. In the absence of algorithms and electronic gadgets, people got creative. Casting lots, rolling dice, or using wheel-like devices called "volvelles" were ancient methods of introducing an element of chance. Fast forward to the Middle Ages, where wheel-like devices evolved into "volvelles," and people continued finding new ways to generate randomness. Drawing straws or picking names from a hat became simple yet effective ways to inject unpredictability into situations. The 20th century ushered in computers, leading to the development of algorithms simulating randomness, giving birth to modern Random Number Generators (RNGs). While the methods evolved, the essence remained the same – creating randomness when needed, now hidden within the circuits of electronic devices.

Understanding the Magic of RNGs
RNGs are like magical machines creating sequences of numbers that appear random. Imagine a friend who loves playing video games; sometimes, the game needs unexpected events, like deciding where a treasure chest appears. That's where Pseudo-Random Number Generators (PRNGs) come in. They follow a plan, called a PRNG algorithm, to create a sequence of numbers that looks random. Here's the twist – they don't start from scratch each time; instead, they begin with a seed, a starting point for the magic. Changing the seed makes the numbers different, much like planting different seeds in a garden. PRNGs have come a long way from ancient lots and medieval volvelles, but the essence remains – creating randomness when needed, now in the hidden circuits of electronic devices.
Real-Life Applications of RNGs: Beyond the Digital Realm
- Cryptography: RNGs are crucial for generating cryptographic keys and initialization vectors, ensuring secure communication and data protection.
- Password Generation: RNGs can be used to generate solid and unpredictable passwords, enhancing the security of user accounts.
- Monte Carlo Simulations: RNGs are extensively used in simulations for modelling complex systems in various fields, such as finance, physics, and engineering.
- Game Development: RNGs are essential for creating unpredictable and dynamic elements in video games, such as random enemy behaviour or item drops.
- Polling and Surveys: RNGs are employed in selecting random samples for surveys and polls to ensure representativity.
- Quality Control: In manufacturing and production, RNGs are used for random sampling to test the quality of products.
- Stock Market: RNGs are used in financial models and simulations to analyze market trends, risk, and uncertainty.
- Option Pricing: In the field of finance, RNGs play a role in the Monte Carlo simulation methods used for option pricing.
- Casinos: RNGs are crucial for ensuring fairness in casino games, determining outcomes randomly and unpredictably.
- Lotteries: Random number generators are used to select winning numbers in lotteries, ensuring a fair and unbiased selection process.
- Experimentation: RNGs are employed in scientific experiments that require randomization, such as assigning subjects to different groups in a clinical trial.
- Data Analysis: RNGs are used in statistical analysis and hypothesis testing to ensure that data is randomly selected for analysis.
- Training Data Shuffling: In machine learning, RNGs are used to shuffle datasets to prevent the model from learning spurious patterns based on the order of data.
- Random Initialization: RNGs are used to initialize the weights of neural networks, helping to avoid convergence to suboptimal solutions during training.
- Search Algorithms: RNGs can be used in randomized algorithms for optimization and searching problems.
- Graph Algorithms: Randomized algorithms are employed in graph theory for tasks such as random graph generation and analysis.
- Software Testing: RNGs are used in software testing to introduce randomness and variability, helping identify potential issues and vulnerabilities.
- Procedural Generation: RNGs are used in creative fields, such as procedural generation in computer graphics and game design, to create diverse and exciting content.
For a diverse range of calculators, make sure to explore CoolCalculator and discover handy tools for various calculations.
Conversation
Latest Blogs
© Blog CoolCalculator, Explore CoolCalculator, your destination for the latest insights, tips, and updates on the world of online calculators. Stay informed and make your calculations smarter with our blog. ,
Designed
by Saad Media Team , Team Lead M.Rizwan Akhtar